Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- gpio
- prescaling
- vivado
- Pspice
- Edge Detector
- KEYPAD
- pwm
- test bench
- structural modeling
- java
- verilog
- Algorithm
- LED
- i2c 통신
- Recursion
- soc 설계
- DHT11
- stop watch
- BASYS3
- ring counter
- FND
- ATMEGA128A
- uart 통신
- hc-sr04
- dataflow modeling
- D Flip Flop
- behavioral modeling
- Linked List
- atmega 128a
- half adder
Archives
- Today
- Total
거북이처럼 천천히
Java - n Queen Problem 본문
1. 문제
- 문제) 한 개의 자연수 N를 입력받은 뒤, N-by-N, 2 dimensional array를 생성하여 N개의 Queen를 배치한다.
단, 어떠한 퀸도 다른 퀸을 위협해서는 안되기 때문에 서로 퀸이 움직일 수 있는 경로상에 퀸이 있어서는 안된다. - 퀸은 상하좌우, 대각선 4방향으로 움직일 수 있다.

2. 생각(Recursion Thinking)
2.1. 들어가기 전
- N개의 말들은 다른 퀸의 경로 상에 있어서는 안되기 때문에 서로 다른 행에 존재할 수 밖에 없으며, N개의 말들을 배치시킬 수 있는 경우의 수는 총 N × N개라고 할 수 있다.
- 문제 해결 방법으로 첫 번째 말을 첫 번째 행에 놓고, 두 번째 말을 다음 행에 놓지만, 첫 번째 말의 경로상에 벗어난 위치에 놓는다. 그리고, 세 번째 말도 다음 행에 놓지만, 첫 번째, 두 번째 말의 경로상에 벗어난 위치에 놓는다. 이 후 말들은 이전 말들의 경로상에 벗어난 위치에 놓을 것이다.
- 만약 말을 놓는 과정에서 조건을 만족하는 위치가 더이상 존재하지 않을 경우, 가장 최근에 놓은 말의 위치를 수정한 뒤, 번복할 것이다. 이러한 BackTracking 알고리즘이라 한다.
2.2. What is Back tracking?
- BackTracking : 해를 찾는 과정에서 더 이상 해를 찾지 못해 문제 해결에 막히면 지나온 궤적(Track)를 다시 돌아가서 가장 최근에 내린 결정을 수정한뒤, 번복하는 과정 및 해결 방법
- 규칙을 따라 차례차례 말들을 놓을 것이지만, Deep-First search과정에서 더 이상의 해를 찾지 못해 되돌아가야 할 상황이 발생할 가능성이 높다. 이를 위해 BackTracking 방법을 이용하여 지나온 궤적을 되돌아가 최근에 내린 결정을 수정한뒤, 이전 과정을 번복(Recursion)할 것이다.
- Deep-First search : 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
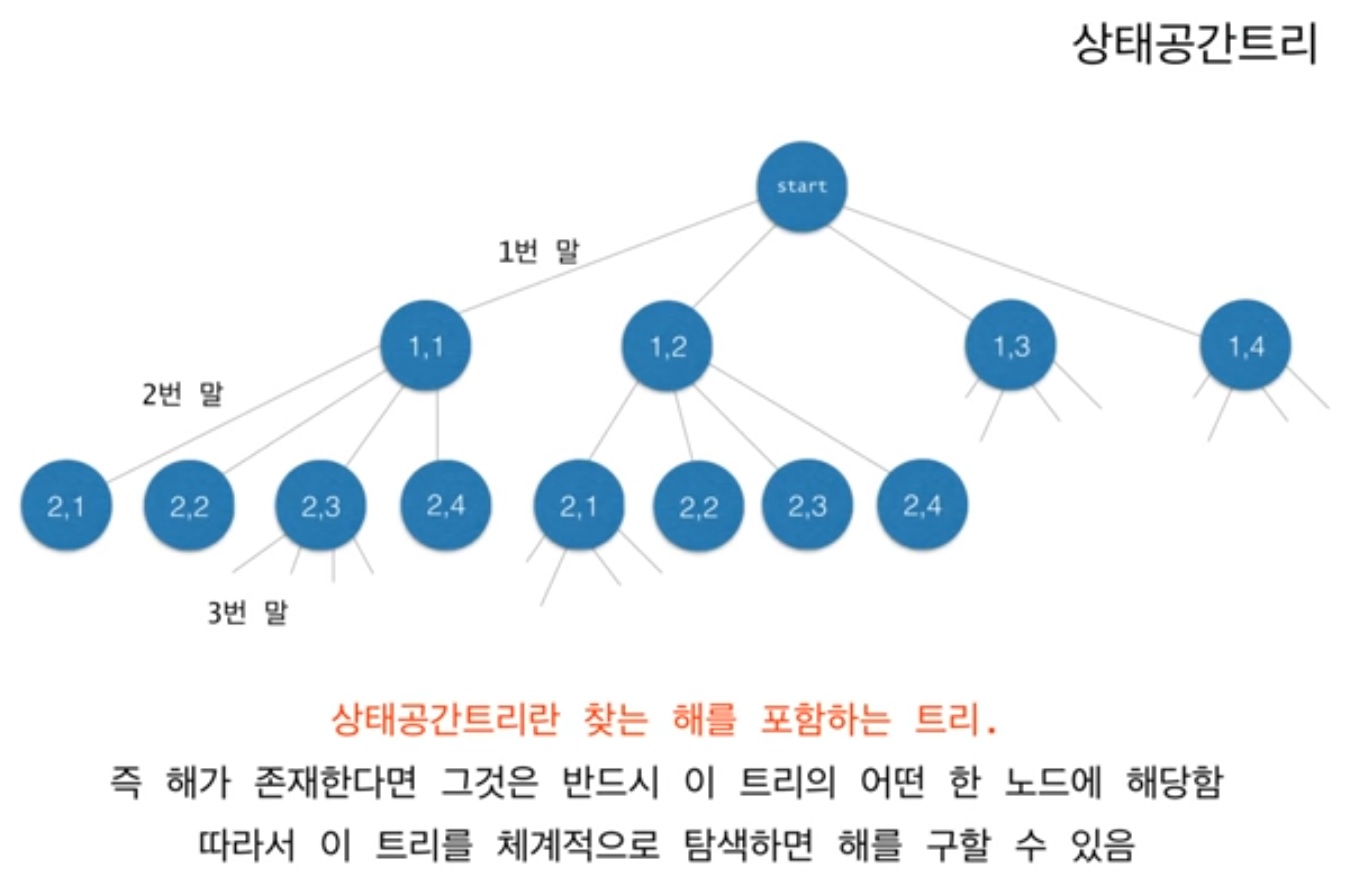
2.3. 상태공간트리(State-space tree)
- State-space tree : state-space tree는 이해를 돕기위해 모든 경우의 수를 트리(Tree) 형태로 표현한 것
- state-space tree는 모든 경우의 수를 표현했기 때문에 해가 존재한다면 해는 반드시 space-state tree안에 하나의 노드로 존재할 것이다. 따라서 state-space tree를 체계적으로 탐색한다면(= 모든 경우의 수를 탐색) 해를 구할 수 있다.
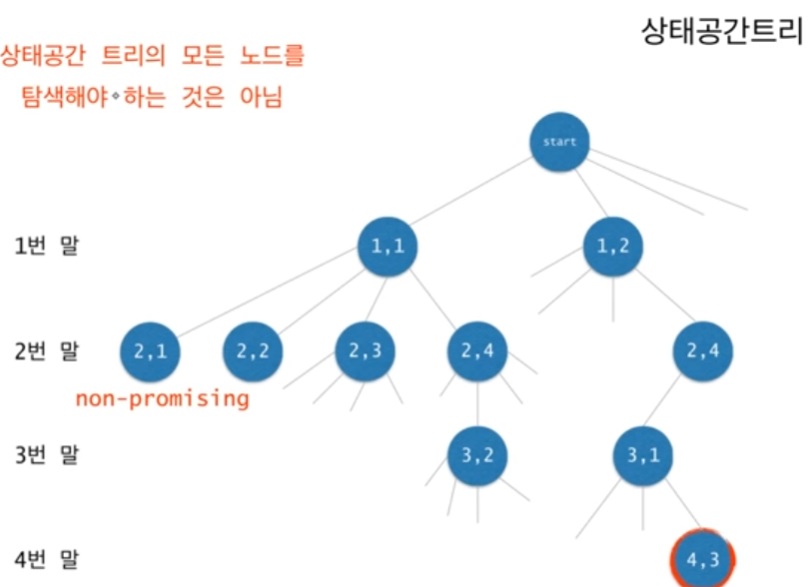
- 하지만, state-space tree의 모든 노드를 탐색할 필요는 없다.
▶ 이미 조건에 부합하지 못한다면, 해당 노드를 탐색할 필요가 없다.
▶ infeasible (in=not + fea=to do, make + sible) : 실행할 수 없는
2.4. 코드 구현
- Backtracking 을 Recursion으로 구현한다면 일반적으로 다음과 같은 구조를 갖게 된다.
Return-type queens(arguments) {
// ** 현재 노드가 infeasible한가?
if non-promising (=infeasible)
report failure and return;
// ** 현재 노드가 최종 답인가?
else if success(=final answer)
report answer and return;
// ** feasible + not final answer = children node에 대해서 recursion
else
visit children node recursively;
}- argument는 현재 셀이 Deep-first search에서 어떤 레벨에 있는지를 알려준다.
- Q) Level 뿐만 아니라 어떤 정보가 필요한가?
▶ 현재 셀의 이전 셀들이 현재 어느 지점에 위치해 있는지에 대한 정보가 필요하다. 그래야지만 경로 상을 벗어난
위치를 선택할 수 있다. 그러나 이전의 셀의 위치는 argument로 전달하기에는 정보량이 방대하기 때문에 그냥
전달하기보다는 Array형태로 묶어서 전달하는 것이 효과적일 것이다.
// *** cols Array는 이전 셀들의 열의 위치를 담고 있다.
// *** ex) cols[i] = j -> Leve i번째 노드는 cols[i][j]에 위치해 있다.
int[] cols = new int[N];
return-type queens(int level) {
if non-promising(=infeasible)
report failure and return;
else if final answer
report answer and return;
else
visit children node recursionly;
}- Q) final answer 조건은 무엇인가?
▶ level argument가 N-1에 도달했다는 것이 final answer이며, level argument가 N-1에 도달했다는 것은 이전 level
에서의 queen 위치들이 서로서로 공격하지 않는 위치에 위치해있다는 것을 의미한다. - Q) infeasible 조건은 무언인가?
▶ infeasible 조건은 두 가지 경우이다. 1) 서로 다른 행의 Queen들이 같은 열에 위치한 경우, 2) 대각선에 위치한 경우
Q1) 같은 열에 위치한지 어떻게 확인하는가?
▶ cols 배열은 queen의 열 값을 담고 있기 때문에 cols 배열을 이용하여 확인하면 된다.
▶ cols[i] == cols[level]
Q2) 대각선에 위치한지 어떻게 확인하는가?
▶ 서로 다른 queen들이 대각선으로 위치했다는 것은 두 queen의 행 값 차이와 열 값의 차이를 비교함으로써 확인
할 수 있다. 행 값 차이와 열 값의 차이가 같다는 것은 두 queen은 대각선으로 위치해있음을 보여준다.
▶ level - i == Math.abs(cols[level] - cols[i]) - 위 내용들을 바탕으로하여 queens 메서드와 infeasible 메서드를 구현하면 다음과 같다.
private static void queens(int level) {
if(isInfeasible(level)) {
return;
}else if(level == n-1) {
addList(); // ** 최종 Queen들의 위치를 List에 저장
return;
}else {
for(int i=0; i<n; i++) {
points[level+1] = i;
queens(level+1);
}
return;
}
}private static boolean isInfeasible(int level) {
for(int i=0; i<level; i++) {
if(points[i]==points[level])
return true;
else if(level-i == Math.abs(points[level]-points[i]))
return true;
}
return false;
}3. 풀이 및 코드 분석
import java.util.Scanner;
import java.util.ArrayList;
public class nQueenProblem {
static ArrayList<int[]> list = new ArrayList<>();
static int[] points;
static int n;
public static void main(String[] args) {
// ** Get n & initialization
n = getN();
// ** Find answers for solving the n-queen problem.
for(int i=0; i<n; i++) {
points = new int[n];
points[0] = i;
queens(0);
}
// ** Print answer
if(list.size()==0)
System.out.println("There is no answer to the n-queen problem.");
else
printList();
}
// *** Get N
private static int getN() {
Scanner scan = new Scanner(System.in);
int input = 0;
while(true) {
System.out.print("Enter N: ");
input = scan.nextInt();
if(input<=0)
System.out.println("N is less than one.");
else
break;
}
return input;
}
// *** Solve the n-queen problem.
private static void queens(int level) {
if(isInfeasible(level)) {
return;
}else if(level == n-1) {
addList();
return;
}else {
for(int i=0; i<n; i++) {
points[level+1] = i;
queens(level+1);
}
return;
}
}
// *** Check for infeasible position.
private static boolean isInfeasible(int level) {
for(int i=0; i<level; i++) {
if(points[i]==points[level])
return true;
else if(level-i == Math.abs(points[level]-points[i]))
return true;
}
return false;
}
// *** Print list.
private static void printList() {
for(int i=0; i<list.size(); i++) {
System.out.printf("List[%d] = {", i);
for(int j=0; j<n; j++) {
if(j==0)
System.out.printf("%d", list.get(i)[j]);
else
System.out.printf(", %d", list.get(i)[j]);
}
System.out.println("}");
}
}
// *** Add new point of queens.
private static void addList() {
int[] newPoints = new int[n+1];
for(int i=0; i<n; i++)
newPoints[i] = points[i];
list.add(newPoints);
}
// *** Initialization of points.
private static void initialization(int level) {
for(int j=level+2; j<n; j++)
points[j] = 0;
}
}Enter N: 6
List[0] = {1, 3, 5, 0, 2, 4}
List[1] = {2, 5, 1, 4, 0, 3}
List[2] = {3, 0, 4, 1, 5, 2}
List[3] = {4, 2, 0, 5, 3, 1}4. 메모
- 첫 backtracking + State-space tree + deep first search 문제이다보니 생각보다 어렵고, 복잡한 문제였다. 많은 연습이 필요할 것으로 예상한다.
'Algorithm > 알고리즘 문제 풀이' 카테고리의 다른 글
| Java - [백준] 15649번 : N과 M (1) (0) | 2022.10.14 |
|---|---|
| Java - 1, 2, 3 더하기 (0) | 2022.10.12 |
| Java - Blob 넓이 구하기 (0) | 2022.10.06 |
| Java - 미로 찾기 (2) | 2022.10.04 |
| Java - 싱글 연결리스트를 통해 다항식 계산 (0) | 2022.08.11 |



