Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- Algorithm
- pwm
- soc 설계
- gpio
- test bench
- KEYPAD
- behavioral modeling
- vivado
- uart 통신
- FND
- atmega 128a
- half adder
- Linked List
- BASYS3
- ATMEGA128A
- ring counter
- i2c 통신
- java
- DHT11
- D Flip Flop
- Pspice
- LED
- verilog
- Edge Detector
- dataflow modeling
- hc-sr04
- stop watch
- prescaling
- structural modeling
- Recursion
Archives
- Today
- Total
거북이처럼 천천히
가산기 본문
1. 반가산기 (Half adder)
- 반가산기는 입력값으로 1bit 크기의 데이터 A, B를 입력받아서 덧셈 연산을 수행 한 뒤, 연산의 결과로 합, Sum과 자리올림, Cout을 출력한다.
- 반가산기는 전가산기와 다르게 자리올림 입력 Cin을 받지 않기 때문에 완전한 가산기는 아니다.
- 반가산기의 진리표는 다음과 같다.

1.1. 반가산기의 회로 구성
- 위 진리표를 토대로 논리식을 Sum of Product으로 표현하면 다음과 같다.
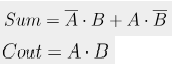
- Half adder의 논리식을 토대로 디지털 논리 회로를 구성하면 다음과 같다.
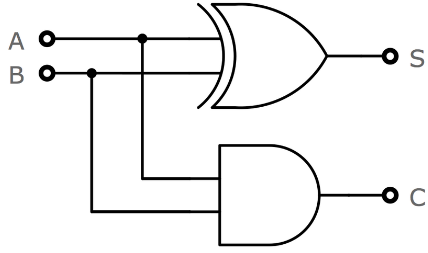
2. 전가산기 (Full adder)
- 전가산기는 입력값으로 1bit 크기의 데이터와 전단의 Carry 값인 Cin을 입력받아서 덧셈 연산을 수행한 뒤, 연산의 결과 값으로 합, Sum과 자리올림, Cout을 출력한다.
- 전가산기는 전단로 부터 Carry 값을 받아 연산하기 때문에 완전한 가산기라고 할 수 있다.
- 전가산기의 진리표는 다음과 같다.

2.1. 전가산기의 회로 구성
- 위 진리표를 토대로 논리식을 Sum of Product으로 표현하면 다음과 같다.

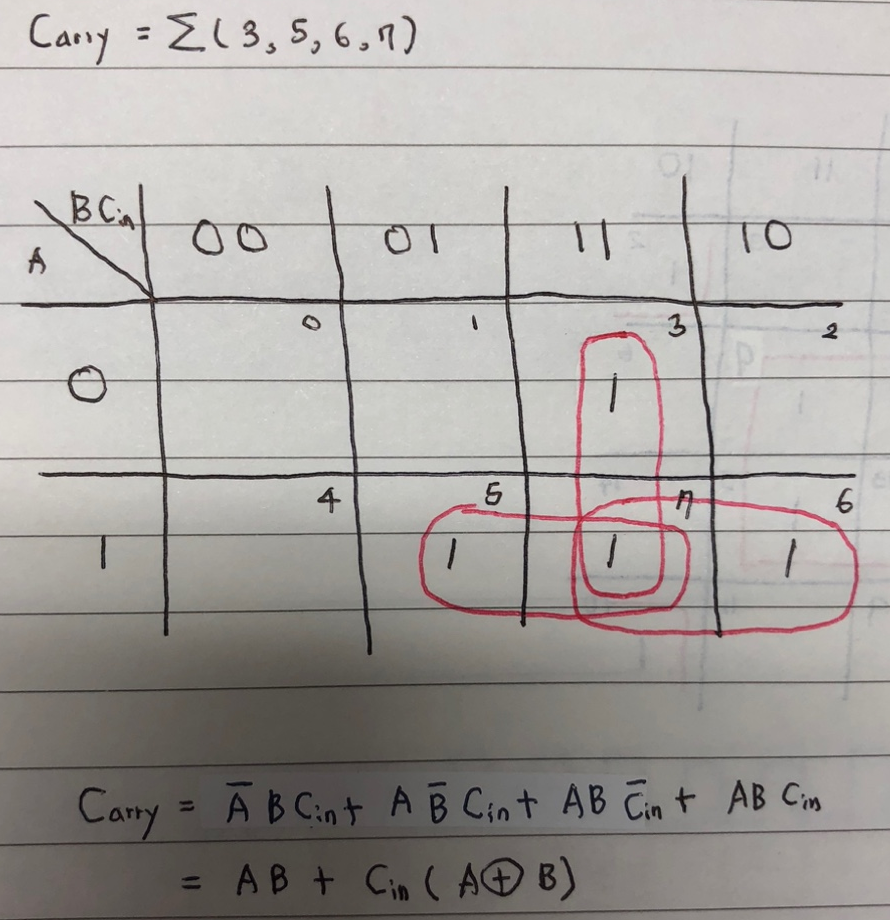
- Full adder의 논리식을 토대로 디지털 논리 회로를 구성하면 다음과 같다.
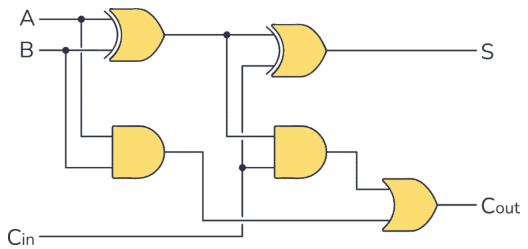
2.2. PSpice를 통한 전가산기의 동작 과정 확인
< 디지털 논리 회로 >
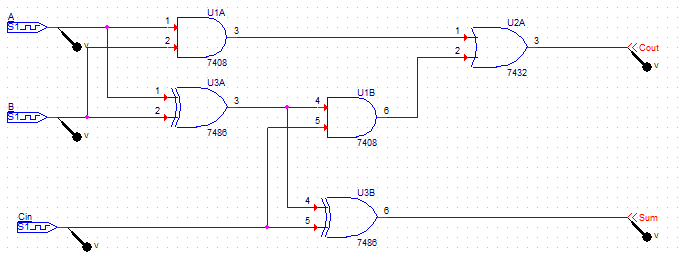
< 시뮬레이션 >
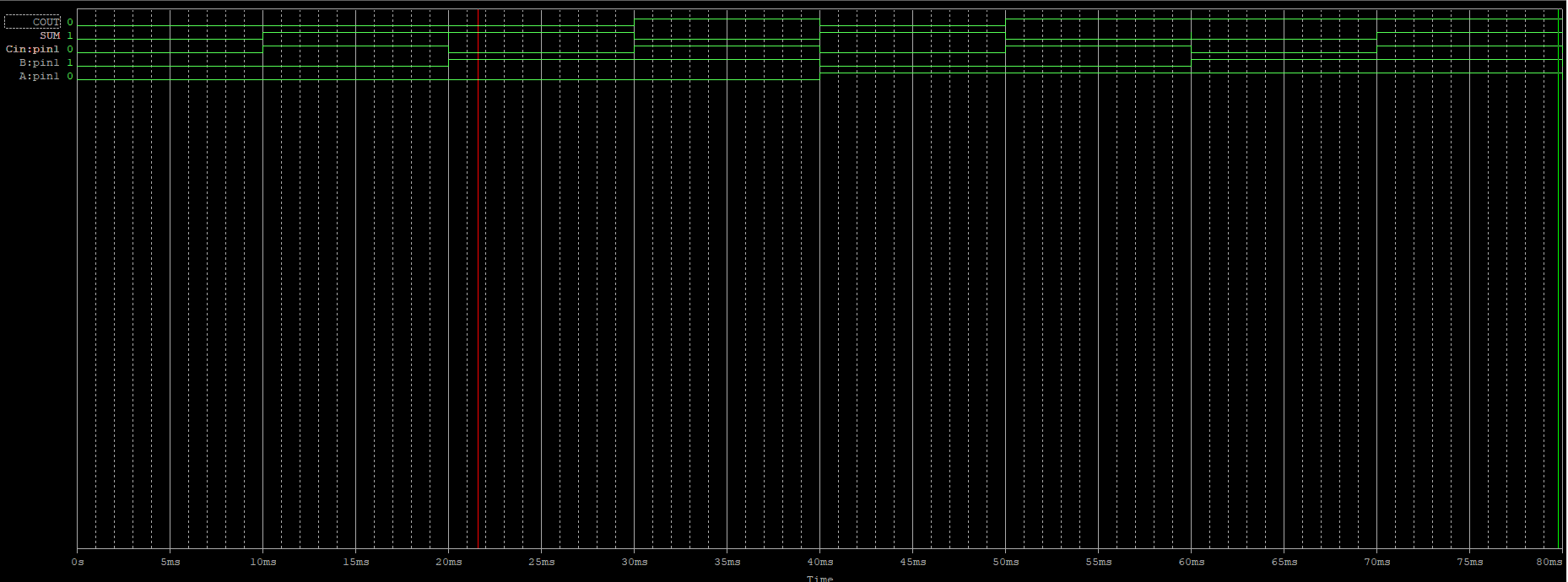

'논리 회로 > 디지털 논리 회로' 카테고리의 다른 글
| 감산기 (0) | 2024.07.03 |
|---|---|
| 4 bit parallel adder (4비트 병렬 가산기) (0) | 2024.07.02 |
| 카르노 맵 (1) (0) | 2024.06.27 |
| 부울 대수, 드 모르강의 정리 (0) | 2024.06.27 |
| 디지털 신호 기초 (0) | 2024.06.26 |




